Binary Search

Binary search is an algorithm to find the position of a target value within a sorted array by recursively halving the number of candidates.

Assuming we have a sorted array with n elements, we can binary search a target element in logarithmic time, O(log(n)). 

Binary Search Algorithm

To perform a binary search on an ordered array, we need to use three pointers:

• mid: a pointer to the middle element of the array, to be used in comparisons, to discriminate whether the target value is in the upper or lower half of the array
• lo: a pointer to the first element of the array, marking the start of the search range
• hi: a pointer to the last element of the array, marking the end of the search range

At each stage, we pick a mid element at position n/2. Then, we compare the value of the mid element with the target.

• If the target is bigger, we continue searching on the right
• if the target is lower than V[mid] we search on the left side
• if the values are matching, we found the target element.

Example of Binary Search

Example: find the index of the array containing the value 14, in the array visible in the image below.

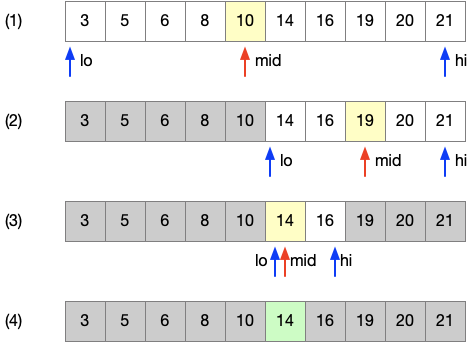
Here is the list of steps to find the target index.

1. we choose a mid element whose value is 10, less than 14. Hence the target must be on the right sub-array.
2. In the new subarray, we choose mid element with value 19, which is greater than 14. We proceed searcing on the left subarray
3. We choose a mid element whose value is 14, which matches the target.
4. We found the target, return its index.

Recursive Implementation

Say we have an array of sorted elements, and we want to find the index of the element with the target value

public int binarySearch(int[] array, int target) {
    return binarySearch(array, target, 0, array.length-1);
}

The most intuitive way to implement binary search is using iteration. For instance, we pass as parameters the array to search, the target value, and the two endpoint indices, as you can see in the implementation below

private static int binarySearchRecursive(int[] array, int target, int lo, int hi){
    if(lo>hi){
        return -1;
    }
    int mid = lo + (hi-lo)/2;
    if(array[mid] == target){
        return mid; // found
    } 
    if(array[mid]<target){
        // search in the upper half
        return binarySearchRecursive(array, target, mid+1, hi);
    } else {
        // lower half
        return binarySearchRecursive(array, target, lo, mid-1);
    }
}

For a recursive implementation, the limit is the growing size of the call stack. For example, in java, we get a Stack Overflow Exception when we go beyond the limit of a few thousand nested calls (~7000).

Iterative Implementation

To avoid the limits of iteration, most of the real-world implementations to work on large-scale systems are implemented recursively.

Implementing the binary search iteratively is pretty straightforward as requires just minor adjustments to the iterative case. See the implementation below.

private static int binarySearchIterative(int[] array, int target, int lo, int hi){
    while(lo<=hi){
        int mid = lo + (hi-lo)/2;
        if(array[mid] == target){
            return mid;
        } 
        if(array[mid]<target){
            // search in the upper half
            lo = mid+1;
        } else {
            // lower half
            hi = mid-1;
        }
    }
    return -1;
}

Resources

Here are a few resources useful to practice on the topic

• https://leetcode.com/problems/binary-search/
• https://www.algoexpert.io/questions/Binary%20Search