Data Structures

Good knowledge of common data structures is needed in computer science.

This article describes common data structures, and present cost and benefits.

Lists

A List is an abstract data type representing a finite collection of ordered elements.

Typically, a List is allocated dynamically depending on the implementation. For example, Array-based lists allocate elements in contiguous memory, and linked lists allocate elements randomly.

Arrays and Array-based Lists

An Array is a collection of elements identified by an index.

An Array provides constant time access to any element in its list. So reading and writing is O(1).

Typically Arrays are statically allocated in a contiguous space of memory, their size is fixed, and the index is zero-based.

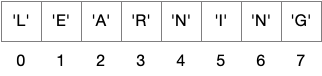
ArrayList and Vector are Array-based lists, providing O(1) access time like Arrays. An additional benefit of these implementations is their size can grow and shrink, and the amortized time for insertion is O(1).

Linked Lists

A Linked List is a sequence of nodes representing contiguous elements.

Typically, the Linked Lists nodes are dynamically allocated. Pointers are used to link nodes, and special pointers to head (first node) and tail (last node) are provided.

In a singly linked list, each node points to the next in the list. In a doubly linked list, each node points both to the next and the previous one.

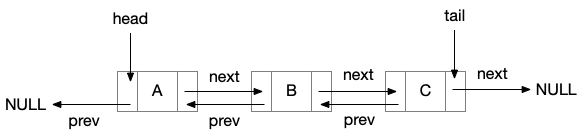
Unlike arrays, don’t provide constant time access to an item, but you can add/remove items from head or tail in constant time.

Stacks

A Stack is a list-based structure that provides restricted access to its elements. The most recent element added is the first to be removed. Hence it has LIFO (Last In, First Out) ordering.

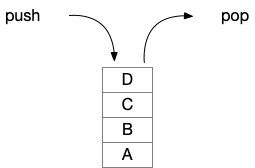
Typically, a stack provides the following operations

• add (or push): add an item to the top of the stack
• remove (or pop): remove and return the item on the top of the stack
• peek (or top): look at the element on top of the stack without removing
• empty: test if the stack is empty

Stacks allow add and remove in O(1) time. Note that, unlike Arrays, Stacks don’t provide constant time access to a random node, but O(N), as in the worst case you need to scan all elements to find the desired one.

Queues

A Queue is a list-based structure that provides restricted access to its elements. The first element added is the first that will be removed, hence it has FIFO (First In, First Out) ordering.

Typically, a queue provides the following operations:

• add (or enqueue): add an item to the tail of the queue
• remove (or dequeue): remove an item from the head of the queue
• peek: look at the item at the head of the queue without removing it

A Queue provides constant time add and remove elements.

Sets

A Set is an abstract data type that stores unique values without ordering.

Typically, a set provides the following operations

• add: add the element if not already contained in the set
• contains: test if the element is already contained in the set
• remove: remove one item from the set
• size: get the number of elements

The HashSet is a commonly used implementation of the Set that provides amortized and average time performance O(1) for basic operations.

Maps

A Map (or Associative Array) is a data structure mapping a key K to a value V. It is used for fast lookups or searching data. It stores data as a <K, V> pair, where a key is unique

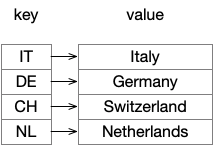
Typically, a map provides the following operations

• put: add the pair <K,V> where the key is unique
• get: return the value V corresponding to the given key K
• remove: remove the pair <K,V> with the given key.
• contains: test if the map contains the given key

The HashMap is a commonly used implementation of the Map that provides amortized constant time performance O(1) for basic operations.

Binary trees

A Tree is a hierarchical tree structure made of nodes. Each node, typically, has a value and a list of references to child nodes. The ancestor of all nodes in a tree is called root.

A Binary Tree is a tree where each node have up to two child nodes.

A Binary Search Tree (BST) is a Binary Tree with a specific property: For each node with a value V, all the left children have values lesser than V, and the right children greater than V.

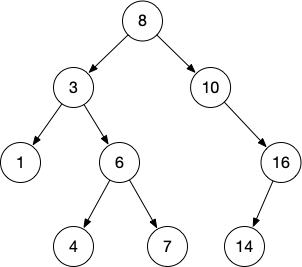
BSTs allow fast lookup, addition, and removal of items. For example, a search on a BST with N nodes takes O(log N) in time.

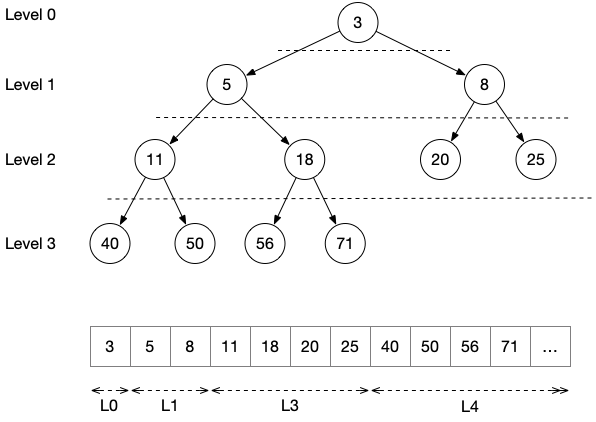
Heaps

A Heap represents an almost complete binary tree that satisfies the heap property. There are two types of Heaps:

• max heap: for any given node the value of the parent is >= than the value of the child
• min heap: the value of a parent is <= w.r.t. the value of a child

Typically, heaps are used to represent priority queues and are implemented as arrays, where the tree structure is computed based on the indices of data in the array.

Graphs

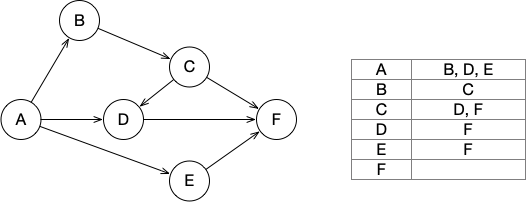
A Graph is a collection of vertices with edges connecting some of the nodes. A vertex is also called a node. A graph is directed when its edges have a specified direction from source to target.

A common way of representing a graph is the adjacency list, where each vertex stores a list of adjacent vertices.

References

• The top data structures you should know for your next coding interview, freecodecamp
• Algorithms, 4th Edition, https://algs4.cs.princeton.edu/24pq/