This article contains a series of exercises on java arrays, including resizing array implementation, merging sorted arrays, etc..
Resizing-array implementation
A Java ArrayList is a resizable-array implementation of the List interface providing amortized-time for insertion of O(1).
Exercise: implement a ResizingArray class providing O(1) amortized-time for insertion.
Growing the array
Basic idea: when the array is full instantiate a larger array, twice the size of the first, and then copy all elements from the first to the new one. Only then, we can insert elements into the resized array.
Note: if we grow the array size of 1 each time we insert a new element, for inserting n elements, we will get a O(n) time complexity. But if we double the size each time the array is full, we get an amortized time complexity of O(1).
O(1) amortized time complexity: consider a resizing array that doubles its size and copies all the old elements each time the array is full. Say we start from an array of size 1, and then, we insert 31 more elements.
- We have 31 insert operations into an array:
O(1)time for inserting - We copy 1+ 2 + 4 + 8 + 16 = 31 elements:
O(1)amortized time for resizing
Hence, we say the total amortized time for insertion is constant, or O(1).
See a sample implementation below:
class ResizingArray{
Object[] values = new Object[1];
int index = 0;
public void add(Object o){
if(index==values.length){
resize(2*values.length);
}
values[index++] = o;
}
private void resize(int capacity){
Object[] copy new Object[capacity];
System.arraycopy(values, 0, copy, 0, values.length);
values = copy;
}
}With this approach, inserting N items into the array takes amortized O(N) time.
Amortized cost of inserting into a resizable array
With this example, if we want to insert N = 16 elements one -by-one, the total cost of insertion will be
| 1 | At initialization |
| 2 | When adding the 3rd element |
| 4 | When Adding the 5th element |
| 8 | When Adding the 9th element |
Merge two sorted arrays
Merge two sorted arrays into a target one, is one of the basic steps of the Mergesort Algorithm. The basic idea here is to keep two indices and increase one or the other depending on the values
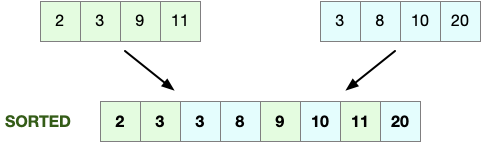
Below you see a typical implementation.
// merge arrays arr1 and arr2 into merged
public void mergeArrays(int[] arr1, int[] arr2, int[] merged){
int i1 = 0, i2 = 0;
for(int i=0; i<merged.length; i++){
if(i1==arr1.length){
merged[i] = arr2[i2++];
} else if (i2==arr2.length) {
merged[i] = arr1[i1++];
} else {
if(arr1[i1]<arr2[i2]){
merged[i] = arr1[i1++];
} else {
merged[i] = arr2[i2++];
}
}
}
}2D array
Multi-dimensional arrays are commonly used in algorithms. In this section, we focus on 2d arrays.
Count the number of islands
This exercise is a classic for coding competitions and interview questions.
Given a 2D array with ‘1’ and ‘0’, where ‘1’ represents land and ‘0’ represents water, count the number of islands. Two cells are connected, so are on the same island, when they share a border in one of the four cardinal directions.
For example, in the image below, we see 6 islands.
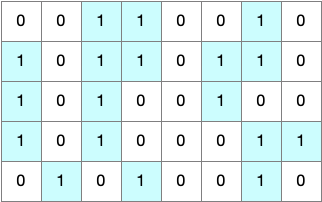
If there are N cells, we can solve the problem with O(n) time and O(n) space complexity.
The basic idea is to scan each cell in the array, and when we find the first ‘1’, we proceed finding all the connected ‘1’ that form an island. While iterating and finding the connected cells, we should make sure to mark the cells as visited, so we won’t visit twice the same cell.
/** time O(ncells) space O(ncells) */
public int countIslands(char[][] grid) {
int count = 0;
// scan all the cells. when find a 1, increment the counter.
for(int row=0; row<grid.length; row++){
for(int col=0; col<grid[row].length; col++){
char cell = grid[row][col];
if(cell=='1'){
count ++;
// transform the connected 1 into a As to mark as visited
paintIsland(grid, row, col);
}
}
}
return count;
}
/** Paint the connected cells recursively */
private static void paintIsland(char[][] grid, int row, int col){
grid[row][col] = 'A';
int maxR = grid.length-1;
int maxC = grid[0].length-1;
if(row>0 && grid[row-1][col] == '1') {
paintIsland(grid, row-1,col);
}
if(col<maxC && grid[row][col+1] == '1'){
paintIsland(grid, row, col+1);
}
if(row<maxR && grid[row+1][col] == '1'){
paintIsland(grid, row+1, col);
}
if(col>0 && grid[row][col-1] == '1'){
paintIsland(grid, row, col-1);
}
}As an example, in the image below, we see the two actions.
- in blue, is represented the iteration until we reach the first island.
- in red, the recursion to find the connected cells.
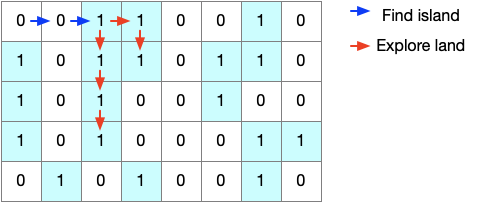
And then, when all the land on the first island is marked as visited (A), we can proceed with the next iterations.
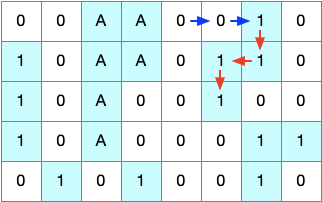

0 Comments