Finite Groups

In this post we provide the definition of finite groups and we show a few examples meaningful for cryptography and blockchain

Def. Finite Groups

Def. A group is a set together with an operation combining two elements of , which satisfies the following properties:

• Closeness: The group operation is closed: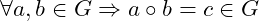
• Associativity: ,
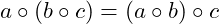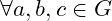
• Identity: there is a neutral elemen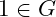t s.t. ,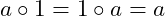
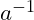• Inverse: , there is an inverse element s.t.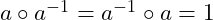

Def. A subgroup of a group is any s.t. is also a group w.r.t. the operation.

Def. A group is called Abelian, or commutative, if satisfies the property

• Commutativity: ,

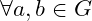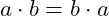
Examples

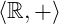1. 2. and 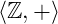are abelian groups: they have identity 0; any element 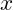has an inverse 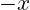, they satisfy associativity, and they satisfy commutativity.
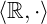2. is not a group: the element 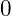has no inverse, and there is nothing we can multiply 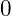to get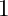
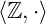3. is not a group: there is no integer we can multiply 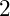by to get to .
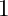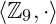4. the set of integers 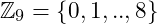together with the operation 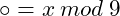, is not a group: the elements 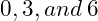don’t have an inverse operation
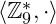5. the set of integers 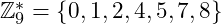( excluding those which does not have inverse), together with the operation 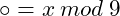, is a multiplicative group.

Multiplicative Groups of Integers Modulo p (Diffie-Hellman)

The Diffie-Hellman key exchange algorithm is based on the multiplicative group of integers modulo a prime number , denoted by . In this context, the group consists of the integers under multiplication modulo .

Example

• Consider 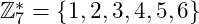, which forms a cyclic group under multiplication modulo 7. This is the basis for the Diffie-Hellman protocol, used for secure key exchange in cryptographic systems, including some blockchain implementations.

Additive Group of Integers Modulo p (Blockchain Consensus Mechanisms)

In blockchain systems, cryptographic hash functions often map inputs to an additive group modulo . This property is used to ensure security and immutability of the blockchain ledger. Cryptographic schemes like RSA also rely on the structure of groups of integers under modulo operations.

Example

• In Bitcoin, the operation of adding transactions into a block involves checking cryptographic hashes that are element of an additive group modulp . This ensures that altering the transaction history is computationally infeasible

Elliptic Curve Cryptography (ECC)

In cryptography, elliptic curves over finite fields form Abelian groups, and they are widely used due to their efficiency and security at smaller key sizes compared to RSA. An elliptic curve group , where is a finite field of prime order , can be used for key exchange, like in the Elliptic Curve Diffie-Hellmann (ECDH), abd digital signatures, like ECDSA