Binary Search Tree (BST)

A Binary Search Tree (BST) is a Binary Tree data structure with nodes ordered according to the following property: For each node with a key K, all the left children have values lesser than K, and the right children greater than K.

BSTs allow fast lookup, addition, and removal of items using the principle of binary search. For instance, searching a node in a balanced binary search tree has an O(log(n)) time complexity.

Balanced Trees

In a balanced binary tree, each node in the tree has two subtrees with about the same number of nodes.

When we search for a key in a balanced binary search tree, for each comparison, we skip about half of the tree by going down one level, either to the left or right subtree.

In the worst case, this takes logarithmic time, that is better than the linear time needed to search an element in an unsorted array.

BST Search

When searching for a key in a BST, we perform a series of comparisons starting from the root node. At each comparison, either the search ends, or we descend one level left or right, thus skipping the branch of the tree where no node can contain the target.

The search ends when we find the target node, or when we can tell that there is no node that can match the target.

Example of BST Search

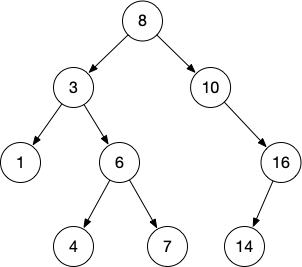
Example: find the node labeled with 6, in the BST visible in the image below.

Here is the list of steps to find the target node.

1. We start from the root node, labeled with 8. Since our target is 6, by BST definition, if there is a node labeled 6, it must be on the left branch.
2. We proceed with the node labeled 3. As we search for 6, the node we search must be on the right branch.
3. Finally, we consider the node labeled 6. This is the Key we are searching, so the search ends.

Note: the example tree has four levels. Hence, in the worst case, we do 4 comparisons before finding the target node or telling such node does not exist.

Note: At each stage of the search, we consider a smaller and smaller sub-tree, until we find the target node. In the worst case, the search takes log(v) time, which corresponds to the number of levels of the tree.

Exercises

In this section, we see a classic coding interview question about Binary Search Trees.

Validate BST

Given a Binary Tree made of connected nodes, determine if it is a valid BST.

Here is a reference implementation of a Node of the BST.

public class Node {
  int value;
  Node left, right;
  public Node(int value){
    this.value = value;
  }
}

Solution

The idea is to find a rule to validate all the nodes of the tree. In this case, we derive the rule from the property of the BST:

Given a node N, with a left and right children, we know:

• The maximum value for all the nodes of the left subtree is the value of the node N
• The minimum value for all the nodes of the right subtree is the value of the node N.

From the rule, we understand that, for each node, we need to know a min/max range for validation. Also, we notice that a root node has no such rance defined. From these considerations, we get to the below implementation.

public boolean isValidBST(Node root){
  return validateRecursively(root, null, null);
}

private static boolean validateRecursively(root, Integer max, Integer min){
  if(n==null){
      return true;
  }
  // a non-null node must respect the rule
  if(min!=null && n.val<=min) return false;
  if(max!=null && n.val>=max) return false;
  // recursion
  if( !isValid(n.left, min, n.val) ) return false;
  if( !isValid(n.right, n.val, max) ) return false;
  
  return true;
}

References

• https://leetcode.com/problems/validate-binary-search-tree/