Algorithms

• Sorting, searching, and binary search
• Divide-and-conquer
• Dynamic programming and memorization
• Greedy algorithms
• Recursion
• Graph traversal, BFS and DFS

Sorting

Main algorithms presented

• Mergesort: Java sort for Objects
• Quicksort: Java sort for primitive types
• Heapsort

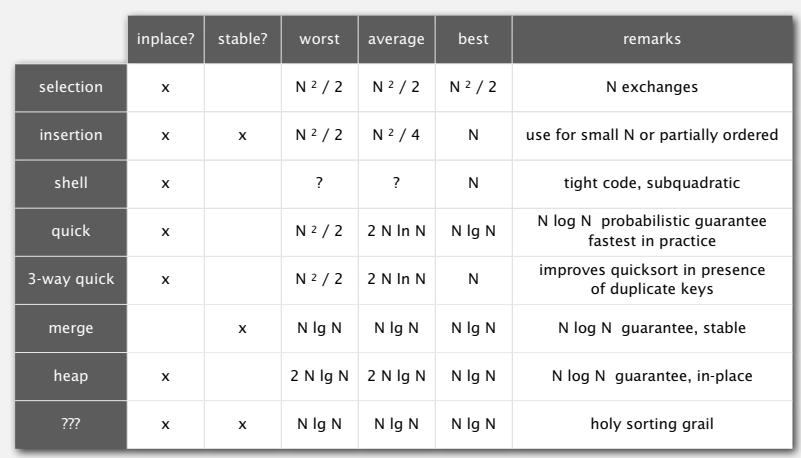
Mergesort vs Quicksort vs Heapsort

All these algorithms have O(N log N) average time complexity, though quicksort is O(N²) in the worst case. In practice quicksort slightly faster than others under given conditions.

• Mergesort: used in Linked Lists with Objects when space is not an issue. Example: Java sorting for Objects
• Quicksort: used in Arrays of primitives, when stability is not an issue. Example: java sorting for primitive types
• Heapsort: used When space is a constraint and can’t tolerate quadratic worst-case performances. Ex: Linux Kernel.

Details are

algorithm	worst	average	best	space	stable
mergesort	O(N log N)	O(N log N)	O(N log N)	O(N)	yes
quicksort	O(N2)	O(N log N)	O(N log N)	O(N log N)	no
heapsort	O(N log N)	O(N log N)	O(N)	O(1)	no

Mergesort

• Stable sorting algorithm: preserves the order
• optimal time complexity: N log N in all cases
• suboptimal in space usage: usage of an extra array for merging

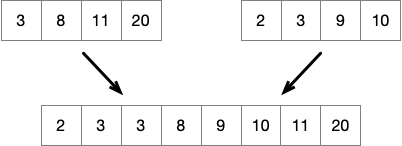
Algorithm

Here is the basic plan

• Divide array in two halves
• Recursively sort each half
• Merge two halves

Algorithm

class MergeSort {
  public static void mergeSort(Comparable[] a){
    aux = new Comparable[a.length];
    sort(a, aux, o, a.length-1);
  }
  /* merge arrays, precondition is arrays are sorted */
  private static void merge(Commparable[] a, Comparable[] aux, int lo, int hi, int mid){
    System.arraycopy(a, aux, 0, a.length);
    int i = lo, j = mid+1;
    for(int k = lo; k <= hi; k++){
      if(i>mid) // end of left array
        a[k] = aux[j++];
      else if(j>hi) // end of right array
        a[k] = aux[i++]; 
      else if(compare(aux[i], aux[j])<0) // 1st left is smaller
        a[k] = aux[j++];
      else {
        a[k] = aux[j++];
      }
    }
  }
  private static void sort(Comparable a[], Comparable[] aux, int lo, int hi){
    if(hi<=lo)
      return;
    int mid = lo + (hi-lo) / 2;// prevent overflow
    sort(a, aux, lo, mid);
    sort(a, aux, mid+1, hi);
    merge(a, aux, lo, mid, hi);
  }
}

Example:

Merging Sorted Arrays

Quicksort

• quadratic complexity in worst case
• linear

A non-stable sorting algorithm, optimal for time and space complexity.

Time Complexity is O(N²)

• shuffle the array A
• partition with a pivot j such that
  • A[j] is inplace
  • all elements left of j are smaller than A[j]
  • all elements right of j are greater than A[j]
• sort each partition recursively

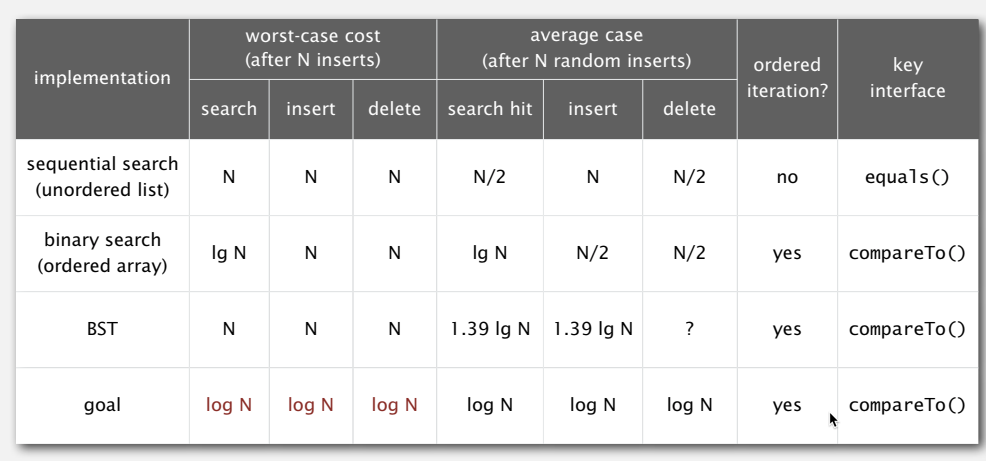
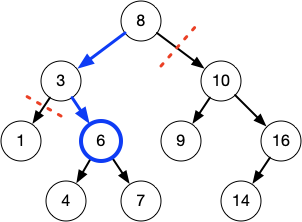
Searching

Binary Search

Trees