This post is a collection of basic topics needed for a proper understanding of Cryptography.
Cryptographic Systems
Primal goal: allow two people to exchange confidential information even if they can only communicate via a channel monitored by an adversary
Symmetric Cryptosystem
A 5-tuple
![]()
Where
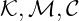 are sets of possible keys, messages, ciphers
are sets of possible keys, messages, ciphers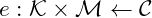 : encryption function
: encryption function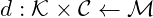 : decryption function
: decryption function
Satisfy ,
, 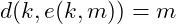
Formal requirements.
- knowing
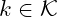 and
and 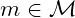 ,
, 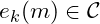 must be easy to compute
must be easy to compute - knowing
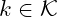 and
and 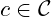 ,
, 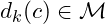 must be easy to compute
must be easy to compute - given one(or more) cypher
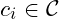 encoded with key
encoded with key 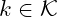 , it must be hard to compute the plaintext(s)
, it must be hard to compute the plaintext(s) 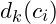
Asymmetric Cryptosystem
A 7-tuple
![]()
Where
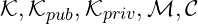 are sets satisfying
are sets satisfying and
and 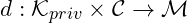 are satisfying
are satisfying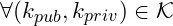 ,
, 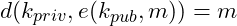
The Discrete Logarithm Problem (DLP)
Let ![]() be a cyclic group with order
be a cyclic group with order ![]() , where
, where ![]() is one of its generators:
is one of its generators: ![]() . The GDLP (Generalized Discrete Logarithm Problem) for the group
. The GDLP (Generalized Discrete Logarithm Problem) for the group ![]() is stated as follows:
is stated as follows:
Given ![]() , find the smallest positive integer
, find the smallest positive integer ![]() such that
such that ![]()
DLP: given a finite abelian group ![]() , and an element
, and an element ![]() generating it, for any
generating it, for any ![]() , compute the smallest positive
, compute the smallest positive ![]() such that
such that
![]()
This
The basic principle
- if we can compute the group operation fast, then from
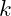 is easy to get
is easy to get 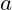
- while, from
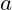 , it is not obvious to get
, it is not obvious to get 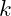
This asymmetry gives us the possibility to build public key cryptosystem.
Indeed, using a finite abelian group, we can build up certain cripto systems whose security rely on the difficulty of the DLP, which depends very much on the group.
Example 1: ![]() is the additive group
is the additive group ![]() of the prime field
of the prime field ![]() , aka
, aka ![]() .
For this case, the DLP is: given
.
For this case, the DLP is: given ![]() and
and ![]() compute the smallest possible
compute the smallest possible ![]() such that:
such that:
![Rendered by QuickLaTeX.com \[a \equiv \underbrace{g + \: \ldots \: + g}_{k \; times} \equiv gk \: mod \: p\]](https://asciiware.com/wp-content/ql-cache/quicklatex.com-8f44a4bc7f185ebfeb47202bf9c4fe7c_l3.png)
In this case the DLP is simple as
Example 2: ![]() is the multiplicative group
is the multiplicative group ![]() of the prime field
of the prime field ![]() , aka
, aka ![]()
In this case, the DLP is: given ![]() and
and ![]() , compute the smallest possible
, compute the smallest possible ![]() such that:
such that:
![]()
Consider the problem of sending an encrypted message through an insecure channel.
- How can two parties A and B can agree on a session key to be used to encrypt and decrypt a message?
Diffie-Hellman Key Exchange
Alice and Bob want to exchange a message. They both know the parameters ![]() ,
, ![]() . They both generate private secret keys
. They both generate private secret keys ![]() and
and ![]() , then compute their public keys as follows:
, then compute their public keys as follows:
- Alice:
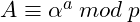
- Bob:
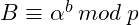
At this point Alice and Bob exchange the public keys, and compute the session key as follows:
- Alice:
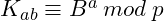
- Bob:
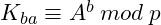
They end up having the same session key: ![]() , which can be used for message encryption.
, which can be used for message encryption.

Proof of correctness
Alice computes: ![]()
Bob computes: ![]()

0 Comments