Mergesort

Mergesort

Mergesort is an efficient and widely used sorting algorithm.

• Stable sorting algorithm: preserves the order
• optimal time complexity: N log N in all cases
• suboptimal in space usage: usage of an extra array for merging

Usage examples:

• Sorting Linked Lists when space is not a concern.
• Java default algorithm for sorting Objects

Basic plan

Mergesort is easier to conceptualize by recursion. Its basic steps are:

• Divide array in two halves
• Recursively sort each half
• Merge two halves

Example

Given the array to sort, we enter the recursion by partitioning the array in halves until we get to the base case, where all the arrays are of size one.

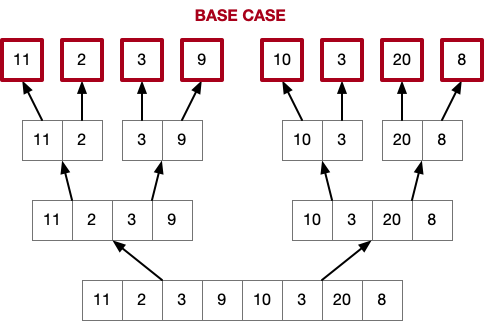
Note: all the arrays of size one are implicitly sorted.

Then, at each step back from the recursion, we merge a pair of sorted arrays into a sorted array twice the size until we get an array of the original size.

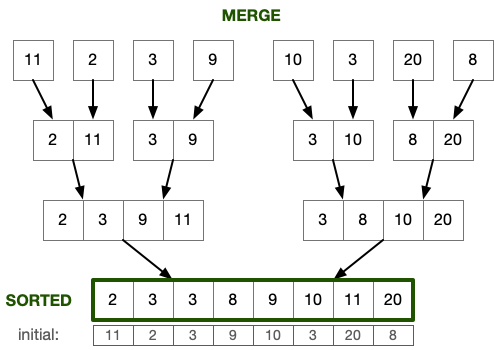
The resulting array is now sorted.

Time and Space Complexity

The time complexity of the algorithm is N log N for all cases. Indeed:

• we have log N levels in the recursion tree
• for each level of the recursion, we compare all the N nodes

The space complexity is O(N) because in practice the algorithm uses an auxiliary array of the same size of the input to perform the merge operation.

Algorithm, Java

In this section, you can see a commented Java implementation for the mergesort algorithm.

At entry point, we initialize an auxiliary array, and start the recursion by sorting the whole input.

  public static void mergeSort(Comparable[] a){
    aux = new Comparable[a.length];
    sort(a, aux, o, a.length-1);
  }

Sorting consists of recursively partitioning the array in halves until we get atomic partitions, which are implicitly sorted (base case). At this point, we can merge the sorted arrays.

  private static void sort(Comparable a[], Comparable[] aux, int lo, int hi){
    if(hi<=lo)
      return;
    int mid = lo + (hi-lo) / 2;// prevent overflow
    sort(a, aux, lo, mid);
    sort(a, aux, mid+1, hi);
    merge(a, aux, lo, mid, hi);
  }

The merge operation reuses the same auxiliary array allocated at the beginning but does the merge using different partitioning indices.

  /* merge arrays, precondition is arrays are sorted */
  private static void merge(Commparable[] a, Comparable[] aux, int lo, int hi, int mid){
    System.arraycopy(a, aux, 0, a.length);
    int i = lo, j = mid+1;
    for(int k = lo; k <= hi; k++){
      if(i>mid) 
        // end of left array
        a[k] = aux[j++];
      else if(j>hi) 
        // end of right array
        a[k] = aux[i++]; 
      else if(compare(aux[i], aux[j])<0) 
        // 1st element on the left smaller than 1st on the right
        a[k] = aux[j++];
      else 
        // 1st on the right is smaller
        a[k] = aux[j++];
    }
  }

Note: we use compare(a, b) meaning it will compare two Comparable objects as a.compareTo(b).

References

• 2.2. Mergesort (web) and 2.2 Mergesort (slides), R. Sedgewick + K. Wayne (Princeton)
• Algorithms: Merge Sort, Gayle L. McDowell (YouTube)